- プリント基板 P板.com TOP
- 技術ネタ・メルマガ
- ［技術情報］エレクトロニクスの確かな情報便
- 高速＆低エラー！差動線路によるGbps伝送プリント基板設計
- 第1回 $S_{21}$で伝送回路の反射量を評価せよ
第1回 $S_{21}$で伝送回路の反射量を評価せよ
高速ディジタル回路=高周波回路！キーワードは「差動」
USB4 ver2 では 40Gbps、PCI-Express Gen6 では 64Gbps というふうに、膨大なデータ通信が可能になりました。
1 秒間に送信するデータ量が多いほど、ディジタル回路の H レベルと L レベルの時間が短くなります。例えば、USB4 ver2 では 39ps、PCI-Express Gen6 では 31ps しかありません。真空中の光でさえ、10mm しか進めない時間です。
これだけの短時間で、H/L レベルを切り替えるためには、振幅電圧を下げるしかありません。しかし、振幅電圧を下げると、外来ノイズの影響を受けやすくなります。
1 つの信号を振幅を半分にし、さらに正相と逆相の 2 つの信号に分けて（通信線も2 本に増やす）伝送する「差動線路」を利用すると、外来ノイズの影響を受けにくくなります。受信端に届いた正相と逆相の信号を差し引いて復元します。2 本の線を撚り合わせておくことで、外来ノイズは 2 本の通信線に同じ位相で重畳するため、ノイズは受信端でキャンセルされて減衰します（図 1）。
本連載では、超高速ディジタル回路に必須の差動線路の特性を理解するために、周波数領域の表現方法である$S$パラメータと特性インピーダンスについて解説します。
第 1 回のテーマは、シングルエンドの$S$パラメータ（Scattering Parameter)、第2 回は差動線路の$S$パラメータです。第 3 回以降は、特性インピーダンスについて解説します。
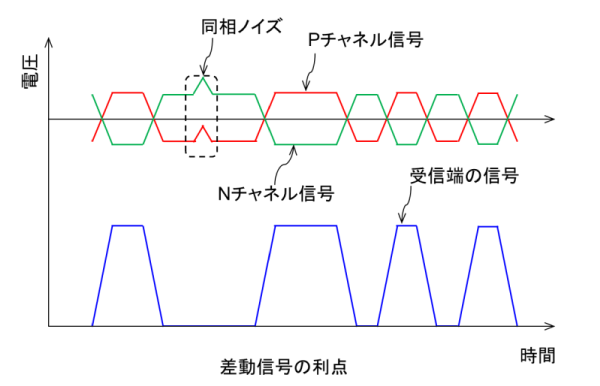
図1 高速信号は差動線路で伝送する。差動線路は低振幅でもノイズの影響を受けにくい
$S$パラメータの基礎知識
入力電圧に掛けると反射電圧が求まる係数
$S$パラメータとは、線形回路網（後述のコラム参照）に交流電力または交流電圧を入力したときの、反射電力（反射電圧）と透過電力（透過電圧）の比を周波数に対して表わしたもので「散乱パラメータ」とも呼びます（図 2）。電子部品や回路、コネクタ、ケーブルの反射や透過を周波数軸で表すことができます。
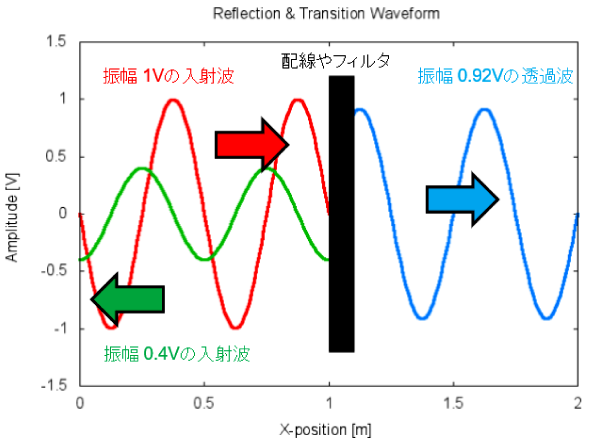
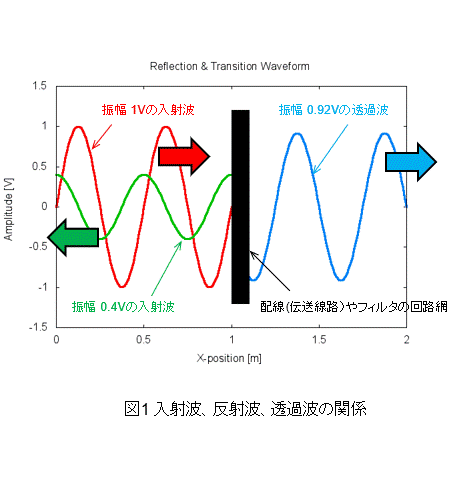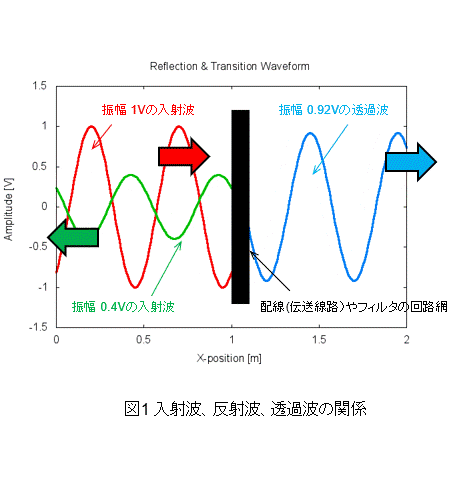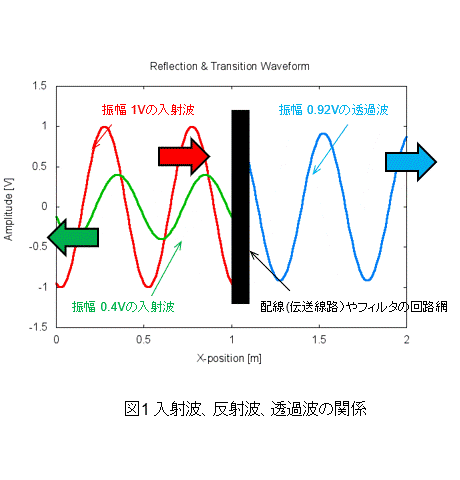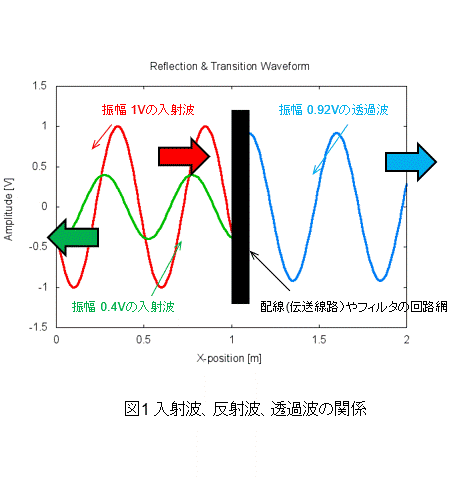
図2 入射波、反射波、透過波の関係。無損失の場合は、$|S_{11}|^2+ |S_{21}|^2=1$の関係があるので、1V の入射電圧に対して、反射電圧が 0.4V（$-$18dB)であれば、透過電圧は、$\sqrt{1-0.4^2}$=0.92（$-$1.7dB)となる
配線やフィルタ（図 2 中央の黒色部）に振幅 1V の波（赤線）が入射すると、反射波（緑線）と透過波（青線）が発生します。反射波が発生する原因は、波源の出力インピーダンスと配線の特性インピーダンス$Z_0$が異なるためです。
この配線や回路の反射特性と通過特性を表す 4 つの係数が$S$パラメータです。反射特性が$-$18dBなら反射電圧は 0.4V、通過特性が$-$17dBなら 0.92V です。なお、$S$パラメータは正弦波に対する応答を示すものです。
パラメータは入力端子と出力端子の入射と反射の計 4 つ
多くの回路や伝送線路は、入出力端子が 1 つずつある 2 ポートの線形回路網で表すことができます（図 3 と図 4）。$S$パラメータは、この回路網を出入りする 4 つの信号の電力比を表すパラメータです。
• $S_{11}$：ポート 1 へ戻る電力とポート 1 から回路網へ入力される電力の比
• $S_{21}$：ポート 2 へ伝わる電力とポート 1 から回路網へ入力される電力の比
• $S_{12}$：ポート 1 へ伝わる電力とポート 2 から回路網へ入力される電力の比
• $S_{22}$：ポート 2 へ戻る電力とポート 2 から回路網へ入力された電力の比
入力部の 2 つの$S$パラメータ
ポート 1（左側の端子）に出力抵抗$50\Omega$をもつ交流電圧源が接続され、ポート 2（図中右側の端子）は$50\Omega$の抵抗で終端しています。
電力を計算するときのインピーダンスは、通常「$50\Omega$」です。ネットワーク・アナライザの入出力インピーダンスも同じく$50\Omega$です。
ポート 1 に入る交流電力は、電圧源出力インピーダンス（$50\Omega$）と回路網の入力インピーダンス（ポート 1 の入力インピーダンス）の差により反射される電力と、回路網を通過してポート 2 へ伝わる電力に分かれます。
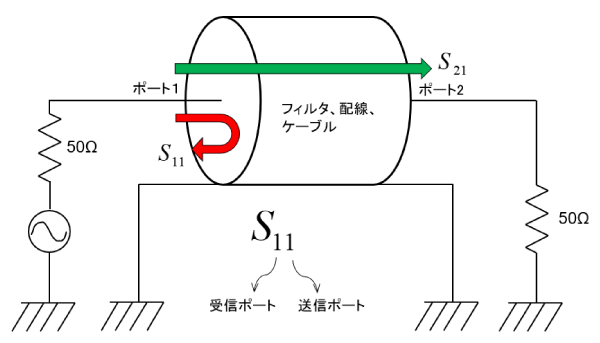
図3 $S_{11}$は反射電圧（電力）$S_{21}$は透過電圧（電力）を示す
$S_{11}$
ポート 1 への入力電力とポート 1 に戻る電力との比です。式 (1) で表します。$S_{11}$の最初の添え字の“1”は電力を受信するポート番号、後の“1”は電力を入力するポート番号です [1]。
\begin{equation} \label{eq:S11} S_{11}=\dfrac{回路網で反射してポート1へ戻る電力}{ポート1から回路網へ入力された電力} \end{equation}
$S_{21}$
ポート 1 に入力した電力が回路網を通過してポート 2 に伝わった電力との比です。式 (2) で表されます。
\begin{equation} \label{eq:S21} S_{21}=\dfrac{ポート2へ伝わった電力}{ポート1から回路網へ入力された電力} \end{equation}
出力部の 2 つの$S$パラメータ
ポート 2（右側の端子）に出力抵抗$50\Omega$をもつ交流電圧源が接続され、ポート 1（左側の端子）は$50\Omega$の抵抗で終端しています。
ポート 2 に入る交流電力は、電圧源出力インピーダンス（$50\Omega$）と回路網の入力インピーダンス（ポートの入力インピーダンス）の差により反射される電力と、回路網を通過してポート 2 へ伝わる電力に分かれます。
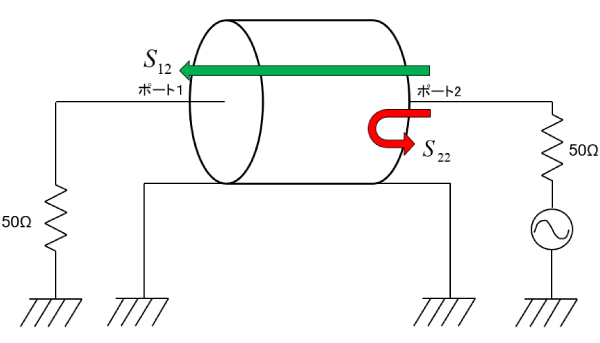
図4 $S_{22}$は反射電圧（電力）$S_{12}$は透過電圧（電力）を示す
$S_{12}$
ポート 2 から入った電力が回路網を通過してポート 1 に伝わる電力との比です。式(3) で表されます。
\begin{equation} \label{eq:S12} S_{12}=\dfrac{ポート1へ伝わった電力}{ポート2から回路網へ入力された電力} \end{equation}
$S_{22}$
2 ポート 2 から入力した電力と、ポート 2 へ戻る電力の比です。式 (4) で表します。
\begin{equation} \label{eq:S22} S_{22}=\dfrac{回路網で反射してポート2へ戻る電力}{ポート2から回路網へ入力された電力} \end{equation}
$S$パラメータの測り方
反射電力比と通過電力比の周波数特性である$S$パラメータを測るときは、あるポートから交流電力を入力して、自分自身のポートへ反射する電力と他のポートへ通過する電力の比を求めます。
$S$パラメータを測るときの基準インピーダンスは「$50\Omega$」です。実際の測定器のインピーダンスも$50\Omega$です。
しかし、フィルタや増幅回路、ケーブルやコネクタのインピーダンスは、必ずしも$50\Omega$ではありません。必要に応じて、ポートのインピーダンス（基準インピーダンス）を読み替える必要があります。実際には、$S$パラメータのビューワなどで、ポート・インピーダンスの読み替えに対応しています。
差動線路用の$S$パラメータ測定器
一般的に、$S$パラメータは、図 5 に示す VNA（Vector Network Analyzer） を使って測ります。TDR（Time Domain Reflectometry）測定器とソフトウェアを組み合わせることでも測定できます。
図5 $S$パラメータはベクトル・ネットワーク・アナライザで測定する。ポートを 4つ備えていれば、差動線路の$S$パラメータも測定できる。複数の差動線路を測るときは、12～16 個のポートをもつネットワーク・アナライザを使う
$S$パラメータの単位は［dB］
$S$パラメータの値は、数桁のレンジで大きく変動するので「対数」で表します。
式 (1)～(4) で求まる値を$x$とすると、対数値は電圧を基準にした場合は式 (5) で、電力基準の場合は式 (6) で表されます。単位は［dB］（デシベル）です。
\begin{equation} \label{eq:Vlog} 電圧基準\quad 20\log_{10}x \quad \mathrm{[dB]} \end{equation} \begin{equation} \label{eq:Plog} 電力基準\quad 10\log_{10}x \quad \mathrm{[dB]} \end{equation}
逆に対数表示された$S$パラメータを通常に比率で表す場合は、電圧基準の場合は式 (7)、電力基準の場合は式 (8) で計算します。
\begin{equation} \label{eq:V10} 電圧基準\quad 10^{\textstyle\frac{x}{20}} \quad \mathrm{[dB]} \end{equation} \begin{equation} \label{eq:P10} 電力基準\quad 10^{\textstyle\frac{x}{10}}\quad \mathrm{[dB]} \end{equation}
表 1 に、$S$パラメータを［dB］と比率で示した具体例を示します。
［dB］を使うと、減衰や増幅率を足し算で計算できます。例えば、ケーブルの$S_{21}$が$-20$dBで、コネクタの$S_{21}$が$-3$dBの場合、全体の $S_{21}$は$-23$dBというふうに求めることができます。
表 1: dB と電圧、電力の関係
| dB | 電圧基準 | 電力基準 |
|---|---|---|
| 40 | 100 | 10000 |
| 20 | 10 | 100 |
| 10 | 3.2 | 10 |
| 6 | 2 | 4 |
| 3 | 1.4 | 2 |
| 0 | 1 | 1 |
| -3 | 0.71 | 0.5 |
| -6 | 0.5 | 0.25 |
| -10 | 0.32 | 0.1 |
| -20 | 0.1 | 0.01 |
| -40 | 0.01 | 0.0001 |
コラム A $S$パラメータの前提は線形回路
線形回路網とは、抵抗やコンデンサ、コイルなどの電流と電圧の関係が比例関係になる素子で構成された回路です。例えば、1V の電圧を加えると、1A が流れ、2V の電圧では 2A の電流が流れる場合は、比例定数が一定となりますので、線形回路網と言えます。1V の電圧に対して 1A、2V に対して 4A の電流が流れた場合は、電流が電圧の 2 乗に比例するため、線形回路網にはなりません。
トランジスタなどの能動素子で構成された回路でも、線形領域を使った動作に限定すれば、線形回路網として取り扱えます。
線形回路網の代表例としてフィルタや増幅回路があります。
ケーブルやコネクタは単体部品ですが、抵抗やコンデンサ、コイルの分布定数回路と考えることができるので線形回路網です。
フィルタは、阻止帯域と通過帯域をもっているため、それぞれの帯域での電力の反射特性、通過特性を$S$パラメータで表現できます。同様に、トランジスタを使った増幅回路の増幅率（周波数に対する）は、通過特性で表現できます。増幅回路の入力段において、特性インピーダンスの不整合による反射特性を$S$パラメータによって表すことが可能です。
ケーブルやコネクタは、入力電力が殆ど通過しそうでので、反射特性や通過特性を考慮する必要がなさそうですが、入力電力の周波数が高くなり、ケーブルやコネクタの物理長に対して入力電力の波長が短くなると、反射が発生します。高い周波数では、表皮効果による導体損や絶縁材がもつ誘電損失により、通過電力が減衰するため、$S$パラメータを使った周波数特性の表現が便利です。
参考文献
[1] Todd Hubing 著、櫻井 秋久ほか訳：デシベルから始めるプリント基板 EMC 即
答 200、ZEP エンジニアリング株式会社。
[2] 電子回路シミュレータ Qucs 公式サイト
