- プリント基板 P板.com TOP
- 技術ネタ・メルマガ
- [技術情報]エレクトロニクスの確かな情報便
- 高速&低エラー!差動線路によるGbps伝送プリント基板設計
- 第2回 反射する基板と反射しない基板
第2回 反射する基板と反射しない基板

$S$パラメータは正弦波が前提
第2回は、$S$パラメータの特性からパルス波形の振幅電圧を計算する方法を紹介します。
$S$パラメータは、高速信号や高周波信号が通過する伝送路や部品、回路の応答を表します。これは、プリント基板やケーブル、電子部品に正弦波を入力したときの反射電力(電圧)比、透過電力(電圧)比です。
$S$パラメータは、正弦波の入力に対する応答なので、一見、パルス状の信号で通信するディジタル回路の設計には役に立たないように思えます。しかし、$S$パラメータのような正弦波に対する回路の応答がわかれば、パルス波形に対する応答もわかります。なぜなら、図1に示すように、パルス波形は、周波数の違う正弦波で合成することができるからです。逆に正弦波の集まりを使って、パルス波形を表すこともできます。これを「フーリエ逆変換」と呼びます。
$S$パラメータからパルス波形に対する応答を求めるときは、通常、回路シミュレータを利用します。しかし、透過電力比((S_{21}))がわかれば、電卓でも簡単に計算できます。
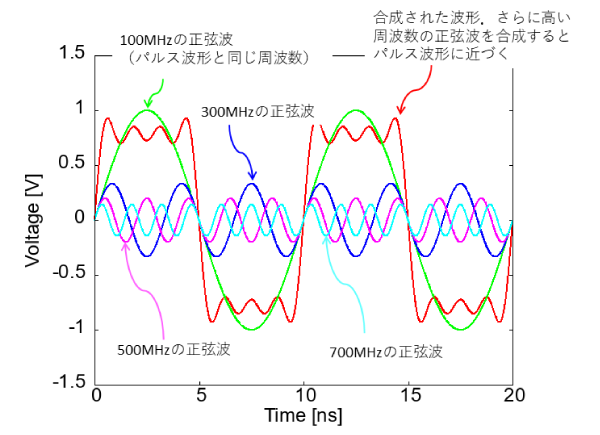
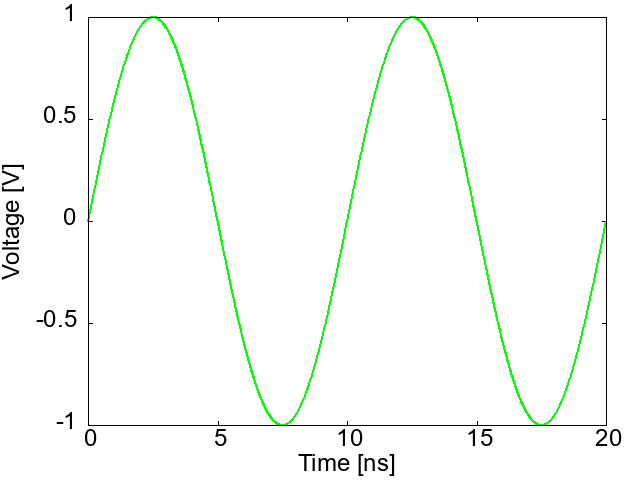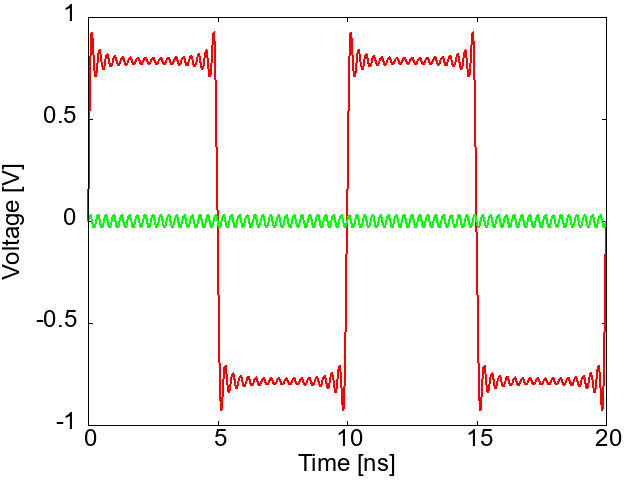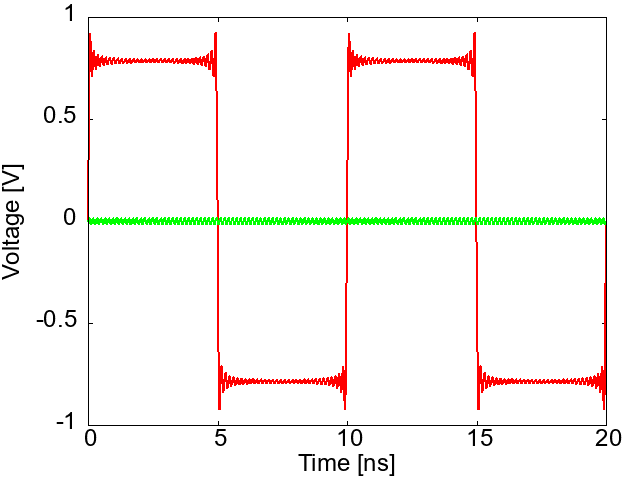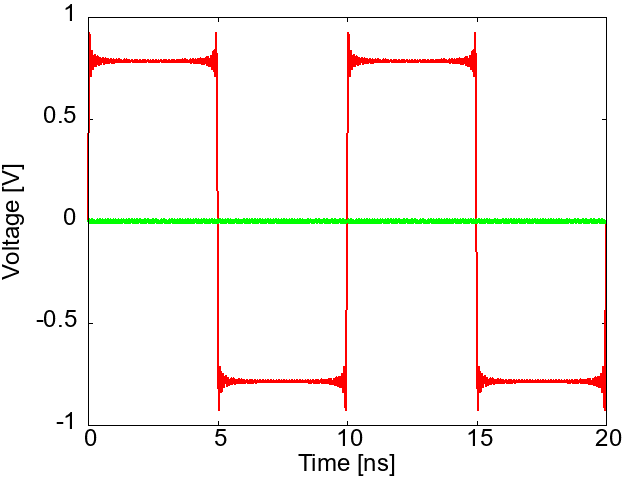
図1 パルス波形を含めどんな波形も正弦波の合成で表すことができる
特性インピーダンスの不連続部は最小限にする
Good!特性インピーダンスの不連続部が少ない基板
4つある$S$パラメータのうち$S_{21}$がわかると、プリント基板やケーブルを通過後の波形を予測できます。
図2に示すのは、特性インピーダンス $Z_0$が異なる4種類の配線が接続された基板です。プリント基板の左端に、1Gbpsのランダム・パルスを発生する電圧源と、$50\Omega$の抵抗を接続します。プリント基板の右端には、$50\Omega$抵抗で終端します。$Z_0$=$50\,\Omega$の配線長は115mm、$Z_0=40\Omega$および$Z_0=70\Omega$の配線長は5mmです。
この基板の終端抵抗$R_L$両端の電圧を観測します。
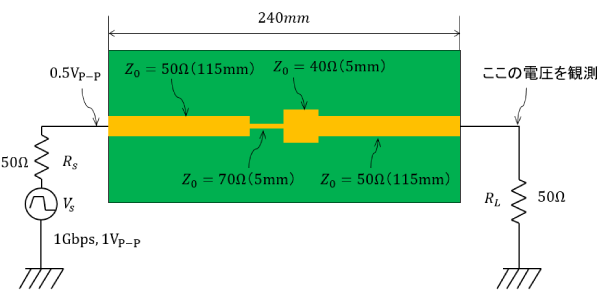
図2 不連続部が短い基板:不連続部は5mm×2。$Z_0=40\Omega$と$Z_0=70\Omega$の配線長は5mm
図3は、図2のプリント基板の$S$パラメータを計算した結果です。
図2のプリント基板は、$Z_0$が$40\Omega$と$70\Omega$の不連続部が5mmと短いため、反射特性を示す$S_{11}$は、3GHzまでは$-20$dB以下です。
表1からわかるように、$-$20dBは10%の電圧が反射するという意味です。$S_{11}$が小さいため、$S_{21}$は直線的に減衰します(図4)。通過特性を示す$S_{21}$がわかると、プリント基板を通過後の波形の振幅電圧を予測できます。
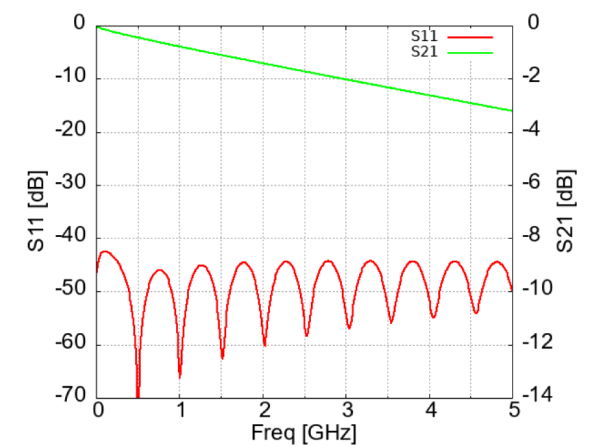
図3 図2の基板の$S_{11}$と$S_{21}$:反射 $S_{11}$が小さいため、$S_{21}$が直線的に減衰する
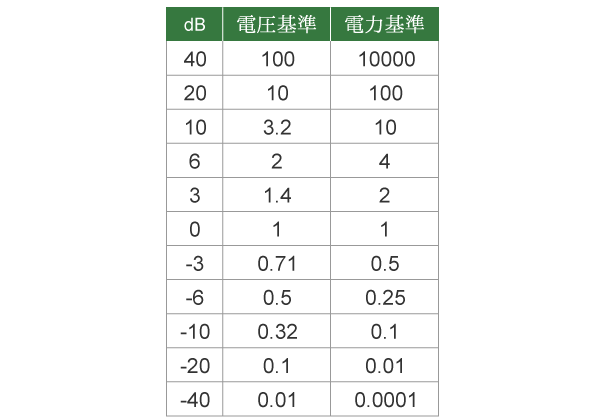
表1 dBと電圧、電力の関係
プリント基板には、1Gbpsの信号が加わっています。1Gbpsは500MHzに相当します。
図3から500MHzの$S_{21}$を読み取ると、$-1.3$dBです。$-1.3$dBは、式\eqref{eq:V10}を使って電圧基準に変換できます。$S_{21}$は入力電圧に対する減衰率です。通過後の電圧は入力電圧を掛けると求まります。0.5を掛ける理由は、プリント基板に入力される電圧が$50\Omega$抵抗で分圧されて0.5Vになるからです。
\begin{equation} \label{eq:V10} 電圧基準\quad 10^{\textstyle\frac{x}{20}} \quad \mathrm{[dB]} \end{equation}
\begin{equation} \label{eq:ex1} 10^{\textstyle\frac{-1.3}{20}} \times0.5=0.43 \mathrm{V} \end{equation}
図4に示すのは、プリント基板を通過した信号の波形です。
実際の波形はランダム・パルスです。すべての波形の状況を観測するために、2nsごとに波形を重ね描きしています。このような波形は、人の目に似ているためため、“Eye-diagram”と呼びます。
Eye-diagramから波形の振幅電圧を求めると、0.437Vです。$S_{21}$から計算した振幅電圧と2%の誤差で一致します。
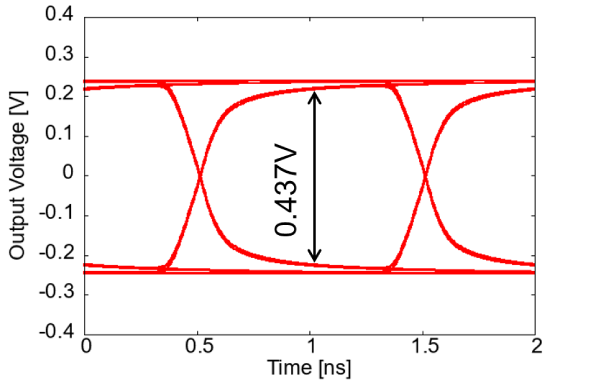
図4 図2の基板のEye-Diagram:$S_{21}$から予測されるEye開口の102%
Bad!特性インピーダンスの不連続部が多い基板
図5は、$Z_0=50\Omega$の配線長が40mm、$Z_0=40\Omega$および$Z_0=70\Omega$の配線長は80mmです。不連続部の配線長が図2より長いです。
この基板の終端抵抗$R_L$の両端の電圧を観測します。
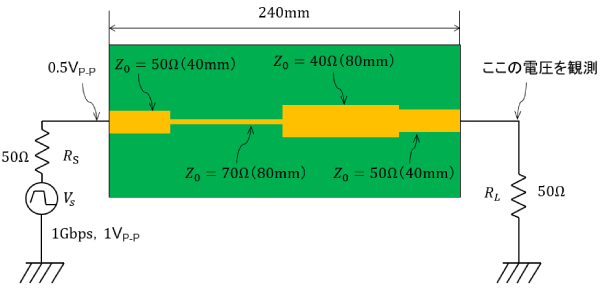
図5 不連続部が長い基板:不連続部は80mm×2。$Z_0=40\Omega$と$Z_0=70\Omega$の配線長は80mm
図6は、図5のプリント基板の$S$パラメータ、図7はEye-diagramです。図4の基板は、$Z_0=40\Omega と 70\Omega$の配線長が80mmと長いため、$S_{11}$が大きく、その影響で$S_{21}$が波打っています(図6)。
線路が無損失ならば、$|S_{11}|^2+ |S_{21}|^2=1$の関係が成り立ちます。反射特性$S_{11}$が大きいと、通過特性$S_{21}$は小さくなります。$S_{21}$を大きくしたい(通過電圧を高くしたい)場合は$S_{11}$を小さくします。$S_{11}$が小さければ$S_{21}$が大きくなり(通過電圧が高くなり)、$S_{11}$が大きければ$S_{21}$は小さくなり(通過電圧が低く)なります。
500MHzにおける$S_{21}$は、図6から$-2.$5dBと読み取れるので、0.5V入力時の基板左端電圧は次のとおりです。
\begin{equation}
\label{eq:ex2}
10^{\textstyle\frac{-2.5}{20}} \times0.5=0.375 \mathrm V
\end{equation}
図7のEye-diagramから振幅電圧を求めると、0.385Vです。誤差3%で一致しています。
$S_{21}$がわかれば、通過波形の振幅電圧を計算できます。$S$パラメータの計算には、無償で無制限に利用できるQucsStudio[2]がおすすめです。
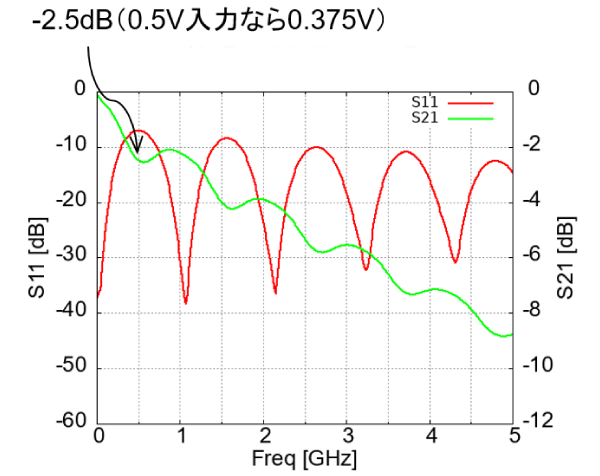
図6 図5の基板の$S_{11}$と$S_{21}$:反射 $S_{11}$が$S_{21}$に影響している
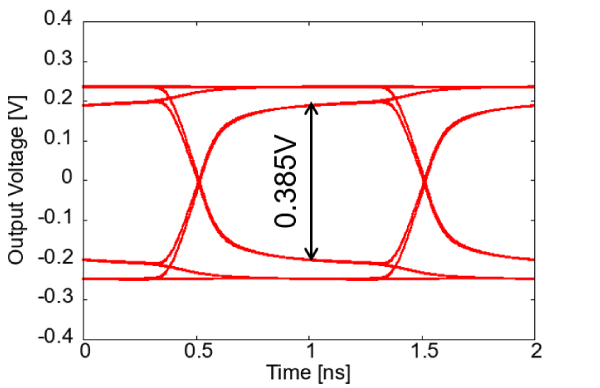
図7 図5の基板のEye-Diagram:$S_{21}$から予測されるEye開口の103%
コラムA 信号源の特性インピーダンスと反射量の関係を調べるなら「$S$パラメータ・ビューワ」
$S$パラメータは、電子部品、配線、ケーブル、コネクタ、フィルタなどの反射と通過を示す係数で、周波数を変数にもちます。
$S$パラメータは、接続される波源の出力インピーダンスや負荷インピーダンス(ポート・インピーダンスと呼ぶ)の影響を受けます。
ポート・インピーダンスが$50\Omega$のネットワーク・アナライザに$75\Omega$の同軸ケーブルを接続すると、反射が大きく計測されますが(図8)、実際には、その$75\Omega$ケーブルをポート・インピーダンスが$75\Omega$の回路網と接続して使うのであれば、$75\Omega$を基準にした$S$パラメータに変換する必要があります。
図9に示すのは、$S$パラメータ・ビューワを使って、$75\Omega$のポート・インピーダンスで読み替えた結果です。$S_{11}$が小さく、$S_{21}$が直線的に減衰することがわかります。
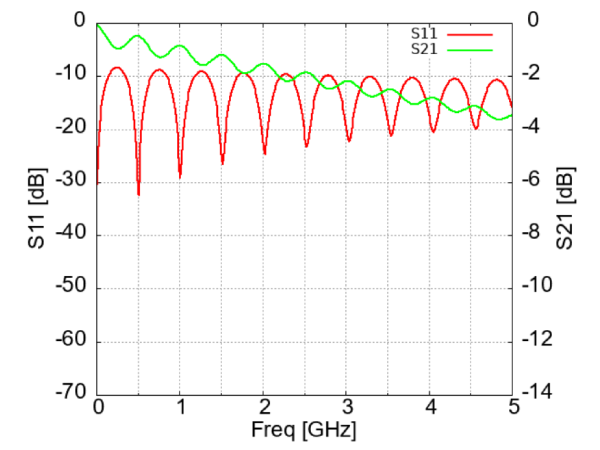
図8 ポート・インピーダンス$50\Omega$の回路網に$75\Omega$同軸ケーブルを接続
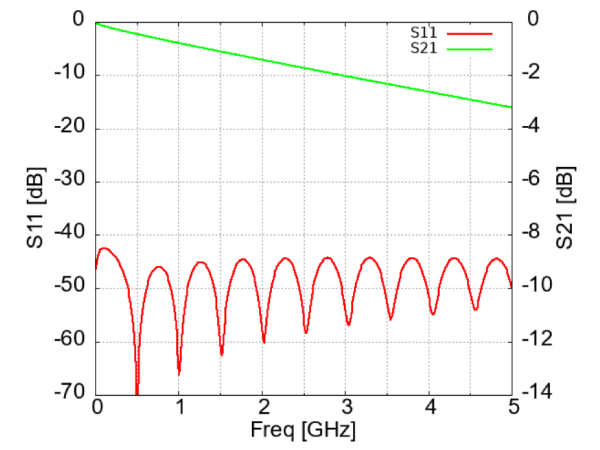
図9 ポート・インピーダンス$75\Omega$の回路網に$75\Omega$同軸ケーブルを接続
参考文献
[1] Todd Hubing 著、櫻井 秋久ほか訳:デシベルから始めるプリント基板 EMC 即
答 200、ZEP エンジニアリング株式会社。
[2] 電子回路シミュレータ Qucs 公式サイト