- プリント基板 P板.com TOP
- 技術ネタ・メルマガ
- [技術情報]エレクトロニクスの確かな情報便
- 高速&低エラー!差動線路によるGbps伝送プリント基板設計
- 第4回 特性インピーダンスの正しい測り方
第4回 特性インピーダンスの正しい測り方

ケーブルやプリント・パターンの特性インピーダンス(Characteristic Impedance:$Z_0$)は、反射波を観測する技術 “TDR”(Time Domain Reflectometry)を利用して、特性インピーダンスの変化点で発生する反射波の電圧を測定し、その電圧値を換算することで求めることができます。
正確なTDR測定には難しさがあります。伝送路に特性インピーダンスの不連続個所が複数あると多重反射が発生して、測定器から離れるほど測定値が不正確になります。本稿では、5つの実験を通じて、問題点と対策を説明します。
特性インピーダンスの正しい測り方
反射電圧を測って換算する
図1 に示すのは、特性インピーダンスの一般的な測定方法です。ステップ・パルスを測定対象に入力して、その反射波形を観測する測定技術“TDR” を利用します。TDRは、ケーブルの断線部や短絡部を見つけるために利用されています。
対象に加えるステップ・パルスの立ち上がり時間を非常に短くし(30ps以下)、電圧方向の分解能を上げていくほど、わずかな特性インピーダンスのずれが検出できるようになります。
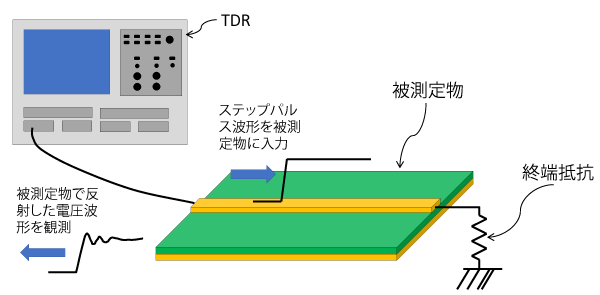
図1 TDR測定とは
ステップ・パルス(200m~250mV)を被測定物に印加して、その反射電圧を測定する技術。横軸は時間であり、インピーダンスの不連続位置を知ることができる。特性インピーダンスは、直接測定して得るのではなく、このTDRで反射電圧を測定し、式(\ref{eq:gamma})と式(\ref{eq:cal_imp})を使って求める
TDR測定の結果から次のような手順で特性インピーダンスを求めます。
まず、式(\ref{eq:gamma})を使って、入力波形と反射波形の比から反射係数$\Gamma$を求めます。さらに、式(\ref{eq:cal_imp})の測定系のインピーダンス$Z_0と$反射係数$\Gamma$の関係式から被測定物の特性インピーダンス$Z_x$を求めます。
\begin{equation} \label{eq:gamma} \Gamma=\dfrac{入力端電圧-入力ステップ・パルス電圧}{入力ステップ・パルス電圧} \end{equation}
\begin{equation} \label{eq:cal_imp} Z_x=\dfrac{1+\Gamma}{1-\Gamma}Z_0 \end{equation}
反射波と終端条件の関係
図2 は、図1 の被測定物をケーブル($Z_0=50\Omega$、遅延時間$\tau$)に変更したときの実験波形です。開放、$50\Omega$、短絡というふうに終端条件を変えています。250mVのステップ・パルス信号を入力し、その反射電圧を観測しています。
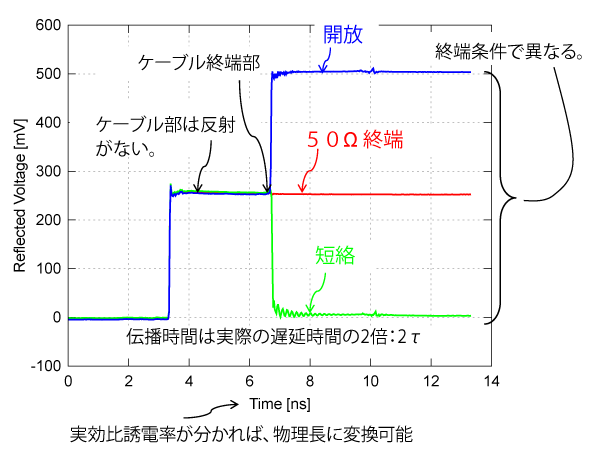
図2 終端条件と反射波(終端条件:開放、短絡、$50\Omega$)
反射波の測定なので、実際の遅延時間の2倍の値が観測される
ケーブル部の特性インピーダンス $Z_0$は、測定器と同じ($50\Omega$)なので反射波がなく、入力パルスと同じ電圧(250mV)が観測されます。ケーブルに入力されたステップ・パルスは約3ns後に終端に到着し、次に示す反射電圧が観測されます。
- 開放終端
終端で入力波形が同じ位相で全反射するため、入力波形と反射波形が合成され、入力波形の2倍の電圧波形が観測される - 50Ω終端
ケーブルの$Z_0$と一致するため、反射は観測されず、終端抵抗で電力として消費されて熱に変わる - 短絡終端
入力波形と逆相の反射波が発生し、入力波形と反射波形が打ち消し合ってゼロになる
測定された反射波は往復時間
ステップ・パルスが終端に到着するまでの時間は3nsです。終端で反射して測定器まで戻る時間なので、ケーブルを通過する時間は半分の1.5nsです。
ケーブル長$l$は、ケーブルの実効比誘電率がわかっていれば、式(\ref{eq:time2dis})から簡単に計算できます。
\begin{equation} \label{eq:time2dis} l=v\cdot \frac{t}{2}=\dfrac{c}{\sqrt{\varepsilon_{eff}}}\cdot \frac{t}{2} \end{equation}
ただし、$v$は被測定物中の電磁波の速度[m/s]、$t$は時間[s](※1)、$c$は光速[m/s]、$\varepsilon_{eff}$は実効比誘電率(※2)です。
反射係数$\Gamma$と特性インピーダンス、反射電圧の関係
表1 に、250mVのステップ・パルス入力時の観測電圧(※3)、観測反射係数、特性インピーダンス、反射電圧の比を示します。計算には式(\ref{eq:gamma})と式(\ref{eq:cal_imp})を使いました。
プリント基板を設計するときは、「特性インピーダンスは$50\Omega\pm 5\Omega$とする」というふうに誤差も指定します。この$5\Omega$のずれは5%ですから、反射波はわずか12.5mV(=250mV $\times$ 0.05)です。
※1 TDRで測定した時間
※2 マイクロストリップライン構造では、上半分が空気であるため実効比誘電率は比誘電率より低い値になる。
$\varepsilon_r=4.2$の場合で$\varepsilon_{eff}=2.9~3.2$
※3 TDR測定器で実際に観測される電圧
表1:反射係数と特性インピーダンス、反射電圧の関係
| 観測電圧[mV] | 反射係数$\Gamma$ | $Z_x[\Omega]$ | 反射電圧[%] |
|---|---|---|---|
| 0 | -1 | 0 | -100 |
| 125 | -0.50 | 17 | -50 |
| 225 | -0.10 | 41 | -10 |
| 238 | -0.05 | 45 | -5 |
| 242 | -0.03 | 47 | -3 |
| 245 | -0.02 | 48 | -1 |
| 250 | 0.00 | 50 | 0 |
| 252 | 0.01 | 51 | 1 |
| 255 | 0.02 | 52 | 2 |
| 258 | 0.03 | 53 | 3 |
| 262 | 0.05 | 55 | 5 |
| 275 | 0.10 | 61 | 10 |
| 375 | 0.50 | 150 | 50 |
| 500 | 1 | $\infty$ | 100 |
正確な反射波を捉えるTDR測定術
正確な特性インピーダンス $Z_0$を得るためには、正確なTDR測定が必要ですが、反射波の観測には難しさがあります。そこで、次に示す5つの実験でTDR測定を行い、うまい反射波の観測技術を紹介します。
- プリント基板単体(図3)
- 2枚のプリント基板をフレキシブル・ケーブル(FPC)で接続し、注入側で反射波を観測(図4)
- 2枚のプリント基板をフレキシブル・ケーブル(FPC)で接続し、終端側で反射波を観測(図5)
- FPC単体(図6)
- FPCを筐体に接続(図7)
実験1:プリント基板単体(図3)の$Z_0$測定
図3 に示すのは、コネクタ、静電気保護用ダイオード(TVS:Transient Voltage Suppressor)を実装したプリント基板の特性インピーダンスです。
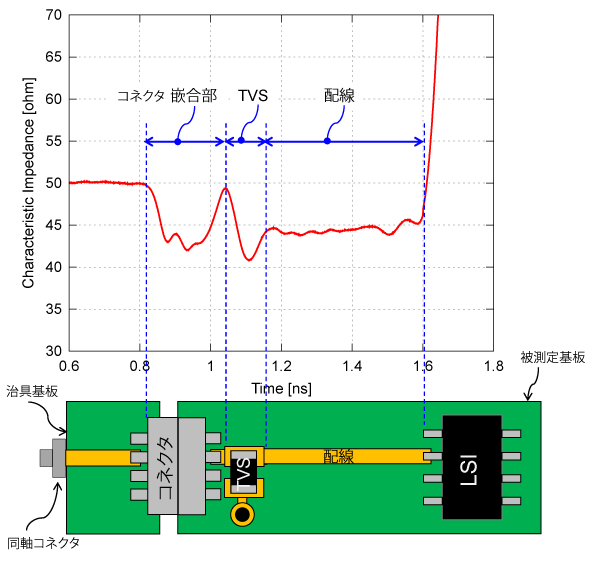
図3 複数の部品が搭載されている
TDR測定器と被測定物を接続するために、同軸コネクタが実装された治具基板を準備し、治具基板とTDR測定器は同軸ケーブルで接続します。
TDRでは反射波を測定するため、被測定物までの経路(治具基板やケーブル)での反射が多いと、多重反射が発生して、被測定物の反射波形をうまく捉えることができません。
そこで、治具基板内部の反射を極力少なくするため、配線や同軸コネクタの実装部も含めて、$Z_0$を極力$50\Omega$に近づけました。同軸コネクタの接続部もはんだ付けではなく、押し付けタイプを利用しました。
図3 のグラフを見ると、治具基板部は$50\Omega$で作られいることがわかります。コネクタ部は、配線の$Z_0$より少し低い$43\Omega$です。
TVSダイオード部は$41\Omega$で、配線部分は$45\Omega$で作られています。LSI部は電源が入っていませんので、ほぼ開放となり、$Z_0$は非常に大きいが観測されます。
この事例では、コネクタやTVSダイオードの特性インピーダンスが$40~45\Omega$なので、配線の$Z_0$を無理に$50\Omega$にする必要はありません。
TDR測定は、横軸が時間なので、基板上の部品位置と$Z_0$と反射の相関が取りやすく、反射が減る対策箇所が直感的にわかります。
実験2、実験3:FPCで接続した2枚のプリント基板の$Z_0$測定
図4 と図5 に示すのは、2枚のプリント基板をFPCで接続した実験回路です。一方の基板にはフィルタが、もう一方の基板にはスルーホールが実装されています。$Z_0$は測定器と基板を接続するための同軸コネクタ部も含めて測定します。
$\blacktriangleright{手前で大きな反射が発生すると遠い位置の反射を捉えられない }$
TDR測定は、反射位置が直感的にわかりますが、手前に大きな反射が発生すると、その先の反射が不鮮明になる欠点があります。
図4 に示すのは、フィルタのある基板側にTDR測定器を接続したときに観測される波形です。
同軸コネクタ部($Z_0=70\Omega$)とフィルタ部($Z_0=28\Omega$)で大きな反射が発生しています。
同軸コネクタ部の反射の要因は、はんだ付けタイプのコネクタを用いたからです。後述しますが、右側の同軸コネクタ部の反射は大きくありません。フィルタ部での反射が大きいため、スルーホールでの反射がほとんど見えません。
TDR測定器を使った特性インピーダンスの測定では、手前に大きな反射が発生すると、遠い位置の反射が多重反射するため正確な測定ができません。
図5 は、スルーホールのある基板側にTDR測定器を接続して測った波形です。
同軸コネクタ部の反射(※4)も少なく、スルーホール部の反射が鮮明になりましたが、フィルタ部分の$Z_0$が$40\Omega$と図4 と比較して反射が小さく観測されています。(※5)
この実験回路は、左右から測定できます。どちらか一方からしかTDRを測定できないこともあります。その場合は、伝送線路や抵抗やキャパシタ、インダクタを回路シミュレータで動かして、実際のTDR波形に合うように定数を調整します。そうすれば、遠い位置にある部品の$Z_0$を予測することも可能でしょう。
※4 同軸コネクタ部のはんだ量が偶然、適切だったのがその理由。はんだ付けタイプの同軸コネクタははんだ量の影響た大きいため取り扱いに注意が必要
※5 $Z_0$の値としては大きいですが、$50\Omega$からのずれが小さいので、反射波の絶対値は小さくなります。
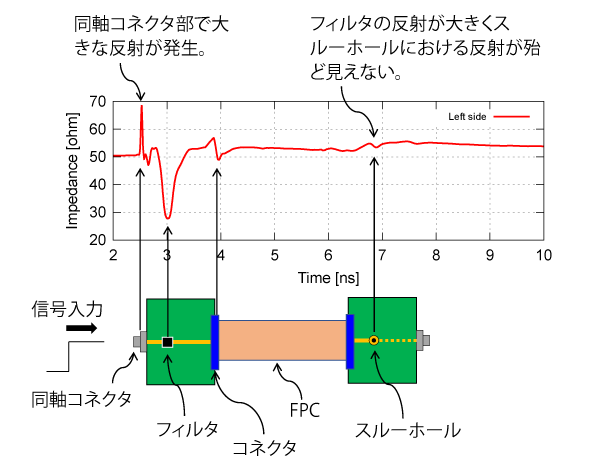
図4 左のフィルタが搭載された基板からTDRを測定
手前で大きな反射が発生すると遠い位置の反射を捉えられない
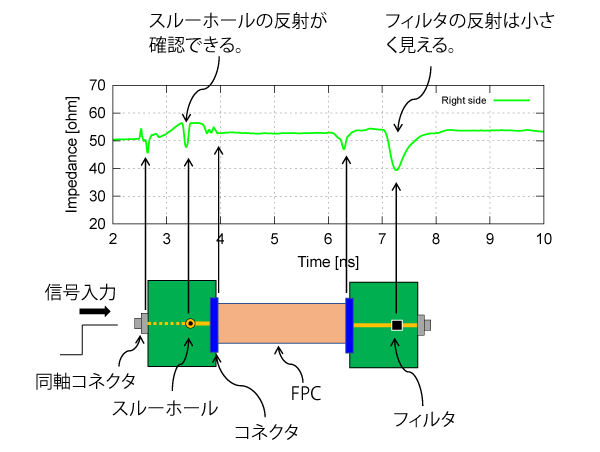
図5 右のスルーホールが実装された基板側からTDRを測定
スルーホール部の反射が鮮明になった
実験4、実験5:筐体に実装されたFPCの$Z_0$測定
FPCやケーブルは、筐体に組み込まれた状態で利用されます。単体では$50\Omega$に整合していた特性インピーダンスが実使用状態で大きくずれることがあります。特に、FPCやプリント基板の配線側は、近くに導体があると、$Z_0$が大きくずれる場合あります。
ここではその例を示します。
図6 は、FPC単体で$Z_0$を測定した結果です。コネクタ部分も含めて$50\Omega$に整合しています。FPCは配線面とGND面の2層構造のマイクロストリップ線路です。
通常、図7 に示すように、FPCは配線面を筐体に固定して使います。この実使用状態では、FPCの固定位置で$Z_0$が$34\Omega$まで低下して、大きな反射が発生します。
対策は、FPCと筐体間に1mm程度の絶縁材を追加して固定し、$Z_0$の低下を防止することです。
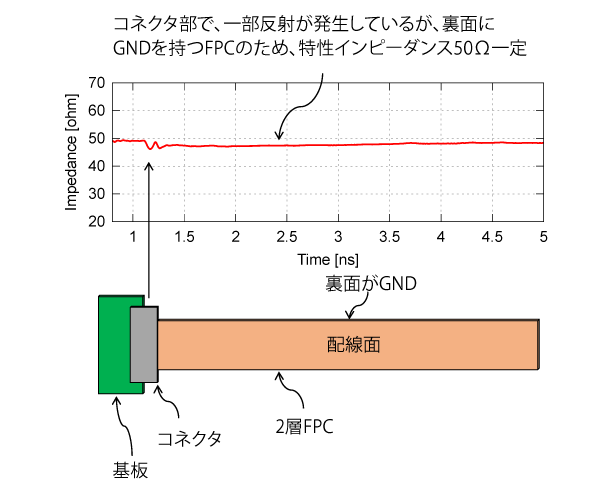
図6 FPC単体では特性インピーダンスはほぼ50$\Omega$一定
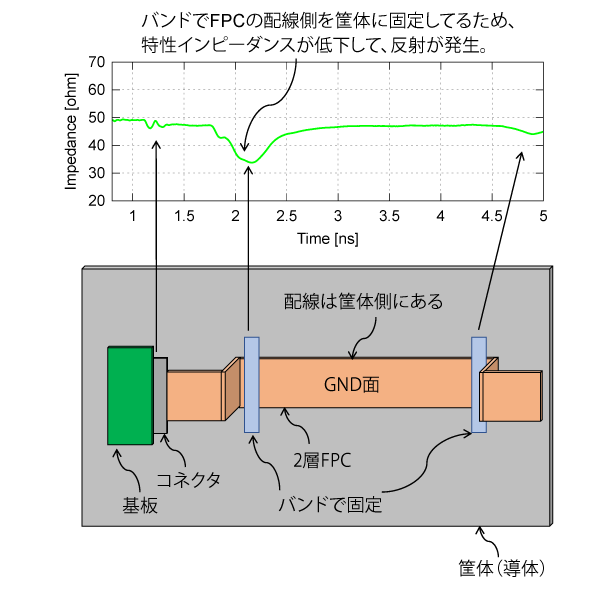
図7 通常、FPCは筐体や基板に接続される。特性インピーダンスが乱れて反射が発生する
参考文献
[1] Todd Hubing 著、櫻井 秋久ほか訳:デシベルから始めるプリント基板 EMC 即
答 200、ZEP エンジニアリング株式会社。