- プリント基板 P板.com TOP
- 技術ネタ・メルマガ
- [技術情報]エレクトロニクスの確かな情報便
- 高速&低エラー!差動線路によるGbps伝送プリント基板設計
- 第5回 差動伝送にはミクスト・モードSパラメータ
第5回 差動伝送にはミクスト・モードSパラメータ

高速ディジタル回路はSパラメータで設計する
なぜSパラメータ?
ディジタル回路の動作クロック周波数が数十MHzと低かった時代は、ロジック回路の間は1本の配線で接続していました。現在では、USBやPCI-Expressに代表されるように、動作周波数は、10Gbps(周波数で言えば、5GHz)を超え、回路間や機器間は「差動」で配線されるようになりました。
クロック周波数の上昇に伴い、配線やケーブル、コネクタ等の受動素子の影響によって信号の波形がひずみ、通信エラーが発生するようになりました。10Gbpsを超える高速ディジタル回路を正しく動かすためには、配線やケーブル、コネクタの設計法を見直す必要があります。
この課題を解決するのは、マイクロ波エンジニアの間では馴染みのある「Sパラメータ」です。これは、線形回路に対する反射特性や通過特性を正弦波に対する応答として評価する指標値です。ディジタル回路のような方形波も、正弦波の合成として表現できるため、ディジタル信号に対する反射や通過の応答を事前に予測することができます。
差動回路用のSパラメータ「ミクスト・モードSパラメータ」
高速シリアル・インターフェースの定番「差動回路」を扱うときは、通常のSパラメータではなく拡張した「ミクスト・モードSパラメータ」を使います。
ミクスト・モードSパラメータを使うと、差動信号に対する反射や損失がわかり、部品選定やプリント基板設計に生かせます。部品メーカのデータシートを読み解く事も可能になります。さらに、差動配線間の構造的な非対称性も表現できるので、放射ノイズの原因などもわかります。
本稿では、昨今の差動回路に拡張したミクスト・モードSパラメータの使い方を解説します。次回第6回は、プリント基板とコモン・モード・チョークを例に、ミクスト・モードSパラメータを実際に使ってみます。
シングルエンド伝送路のSパラメータ表現
第1回で配線が1本の場合の2ポートSパラメータを解説しました。2ポートSパラメータは、複数の配線に対して拡張可能です。
図1 に示すように配線が2本ある場合、信号の出入り口は4つなので、4ポートのSパラメータで表現します。配線が3本あれば6ポート、4本あれば8ポートSパラメータです。
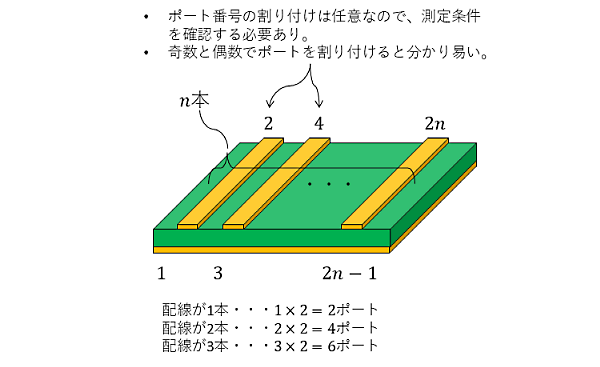
図1 配線の本数とポート数の関係
4ポートのSパラメータは$S_{11}$、$S_{12}$、$S_{13}$、$S_{14}$…$S_{44}$までの合計16個(=4×4)です。Sパラメータの添え字の意味は、2ポートSパラメータの拡張になるため、受信部がポート1の場合は次のとおりです(図2)。
- $S_{11}$:ポート1に交流電圧(電力)を入力した時のポート1への反射電圧比
- $S_{12}$:ポート2に交流電圧(電力)を入力した時のポート1への通過電圧比
- $S_{13}$:ポート3に交流電圧(電力)を入力した時のポート1への通過電圧比(近端クロストーク)
- $S_{14}$:ポート4に交流電圧(電力)を入力した時のポート1への通過電圧比(遠端クロストーク)
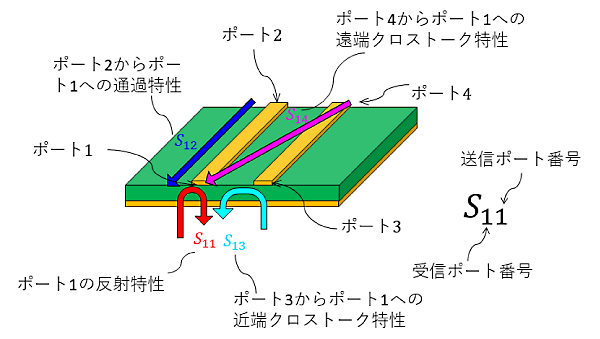
図2 シングルエンドSパラメータ(4ポート)。送信ポート番号と受信ポート番号の組合わせでSパラメータを示す
これらの組み合わせが、ポートごとにあります。$S_{22}$はポート2の反射特性、$S_{21}$はポート1からポート2への通過特性、$S_{23}$はポート3からの遠端クロストーク特性、$S_{24}$はポート4からの近端クロストーク特性です。
差動伝送線路のSパラメータ表現
2本の配線を1本にまとめて表す
USBやPCI-Express、HDMIは、2本の配線を使って差動信号を伝送します。差動信号は、同相ノイズを相殺できるので、振幅電圧を下げることができ、LからHへの遷移電圧が小さくてすむため、動作クロック周波数の高いディジタル通信が可能です。
差動信号配線では、逆相の方形波が伝送されるため、逆相信号が通る配線の応答もSパラメータで表す必要があります。
差動線路の場合は、2本の配線を1本の配線として考え、逆相(差動)信号と同相信号に対する応答で表現したミクスト・モードSパラメータを利用します(図3)。
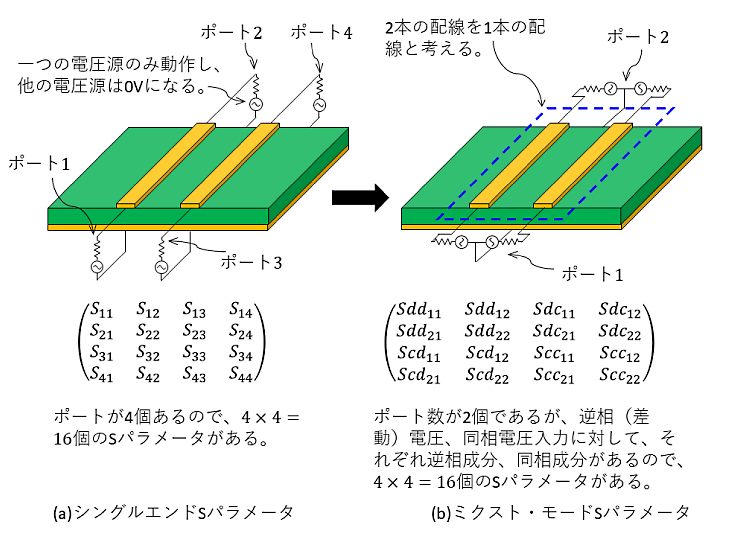
図3 シングルエンドSパラメータとミクスト・モードSパラメータ
16個の変数を扱う
ミクスト・モードSパラメータでは、図3(b)に示すように、ポート1とポート3をポート1にポート2とポート4をポート2と再定義し、それぞれのポートに逆相または、同相の電圧を加えて、反射電圧比(シングルエンドの$S_{11}$に相当)や透過電圧比($S_{21}$)を測定します。
ミクスト・モードSパラメータでは、反射と透過電圧が逆相電圧と同相電圧の2とおりです。したがって、以下の16とおりの組み合わせがあります。
表1:各$S$パラメータの説明
| 項目 | 説明 |
|---|---|
| $S_{dd11}, S_{dd22}$ | 逆相電圧入力、逆相電圧反射比 |
| $S_{dd21}, S_{dd12}$ | 逆相電圧入力、逆相電圧透過比 |
| $S_{cd11}, S_{cd22}$ | 逆相電圧入力、同相電圧反射比 |
| $S_{cd21}, S_{cd12}$ | 逆相電圧入力、同相電圧透過比 |
| $S_{dc11}, S_{dc22}$ | 同相電圧入力、逆相電圧反射比 |
| $S_{dc21}, S_{dc12}$ | 同相電圧入力、逆相電圧透過比 |
| $S_{cc11}, S_{cc22}$ | 同相電圧入力、同相電圧反射比 |
| $S_{cc21}, S_{cc12}$ | 同相電圧入力、同相電圧透過比 |
添え字「d」は逆相成分、「c」は同相成分を表し、数字はポート番号です。添え字「dd」の最初の「d」は受信ポートの成分、2番の「d」は送信ポートの成分を示し、添え字「21」の最初の「2」は受信ポートの番号、2番の「1」は送信ポート番号になります。$S_{dd21}$はポート1から逆相電圧を入力して2へ透過した逆相電圧比です。
求め方
実際のミクスト・モードSパラメータは、シングルエンドのSパラメータを測定後、式1を使って計算します。
\begin{equation} \label{eq:Spara1} \begin{aligned} & \scriptsize{ \begin{pmatrix} S_{dd11} & S_{dd12} & S_{dc11} & S_{dc12} \\ S_{dd21} & S_{dd22} & S_{dc21} & S_{dc22} \\ S_{cd11} & S_{cd12} & S_{cc11} & S_{cc12} \\ S_{cd21} & S_{cd22} & S_{cc21} & S_{cc22} \\ \end{pmatrix} }= \\ &\dfrac{1}{2} \scriptsize{ \begin{pmatrix} S_{11} - S_{13} - S_{31} + S_{33} & S_{12} - S_{14} - S_{32} + S_{34} & S_{11} + S_{13} - S_{31} - S_{33} & S_{12} + S_{14} - S_{32} - S_{34} \\ S_{21} - S_{23} - S_{41} + S_{43} & S_{22} - S_{24} - S_{42} + S_{44} & S_{21} + S_{23} - S_{41} - S_{43} & S_{22} + S_{24} - S_{42} - S_{44} \\ S_{11} - S_{13} + S_{31} - S_{33} & S_{12} - S_{14} + S_{32} - S_{34} & S_{11} + S_{13} + S_{31} + S_{33} & S_{12} + S_{14} + S_{32} + S_{34} \\ S_{21} - S_{23} + S_{41} - S_{43} & S_{22} - S_{24} + S_{42} - S_{44} & S_{21} + S_{23} + S_{41} + S_{43} & S_{22} + S_{24} + S_{42} + S_{44} \\ \end{pmatrix} }\end{aligned} \end{equation}
ミクスト・モードSパラメータの各値の意味
$S_{dd11}$と$S_{dd21}$
$S_{dd11}$は、逆相電圧入力時の逆相電圧の反射比です。
図4 に示すようにポート1とポート3にそれぞれ逆相電圧を入力し、ポート1とポート3の電圧の差を測定します。この電圧差から入力電圧を差し引けば、逆相の反射電圧が計算でき、入力電圧と反射電圧の比が$S_{dd11}$です。
$S_{dd21}$は逆相電圧入力時の逆相の透過電圧比です。ポート2とポート4の電圧の差から逆相透過電圧がわかるので、入力電圧との比を計算すれば、$S_{dd21}$が求まります。ちなみに、配線間隔が広く結合が無い場合は、$S_{11} = S_{33} = S_{dd11}、 \quad S_{21} = S_{43} = S_{dd21}$ です。
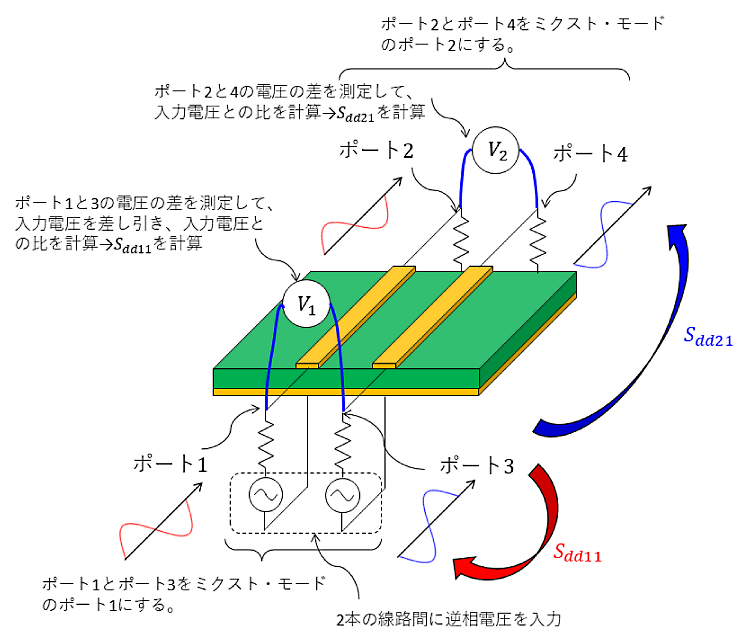
図4 $S_{dd11}$と$S_{dd21}$の測定法。$S_{dd11}$:逆相交流電圧入力に対する逆相の反射係数。$S_{dd21}$:逆相交流電圧入力に対する逆相の透過係数。
$S_{cd11}$と$S_{cd21}$
$S_{cd11}$は、逆相電圧入力時の同相電圧の反射比です。$S_{cd21}$は逆相電圧入力時の同相の透過電圧比です。
図5 に示すように逆相の電圧入力に対して、同相の反射成分や同相の透過成分の比率を示します。同相成分はポート1(またはポート2)とポート3(またはポート4)間の電圧和を測って求めます。
配線の構造が完全に対称であれば、$S_{cd11}$、$S_{cd21}$はゼロになります。配線長が異なれば、電圧和がゼロにはならないので、同相成分が発生します。配線長が同じでも、2本の配線幅が異なれば、遅延時間が同じならないので、やはり同相成分が発生します。
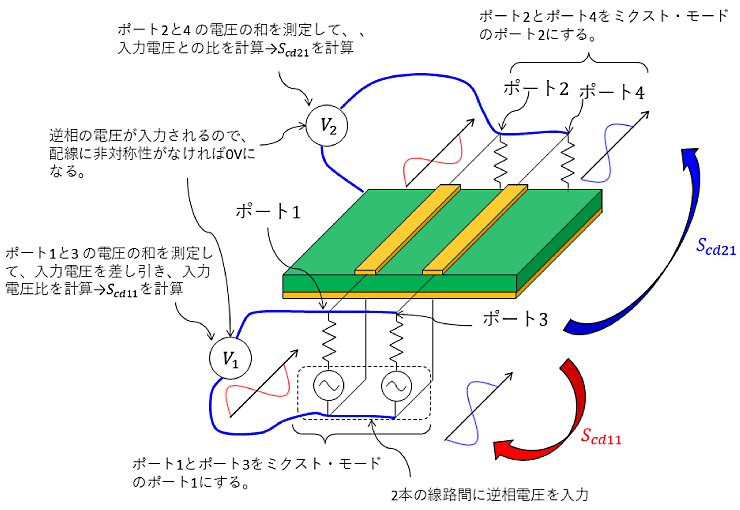
図5 $S_{cd11}$と$S_{cd21}$の測定方法。$S_{cd11}$:逆相交流電圧入力に対する同相の反射係数。$S_{cd21}$:逆相交流電圧入力に対する同相の透過係数。
$S_{cc11}$と$S_{cc21}$
図6 に示すように、$S_{cc11}$は同相電圧入力時の同相電圧の反射比、$S_{cc21}$は同相電圧入力時の同相の透過電圧比です。同相成分は$S_{cd}$を求めた時と同じように、各ポート間の電圧和を計算します。$S_{dd}$と同様に配線間の結合が無ければ、$S_{11}=S_{33}=S_{cc11}、S_{21}=S_{43}=S_{cc21}$です。
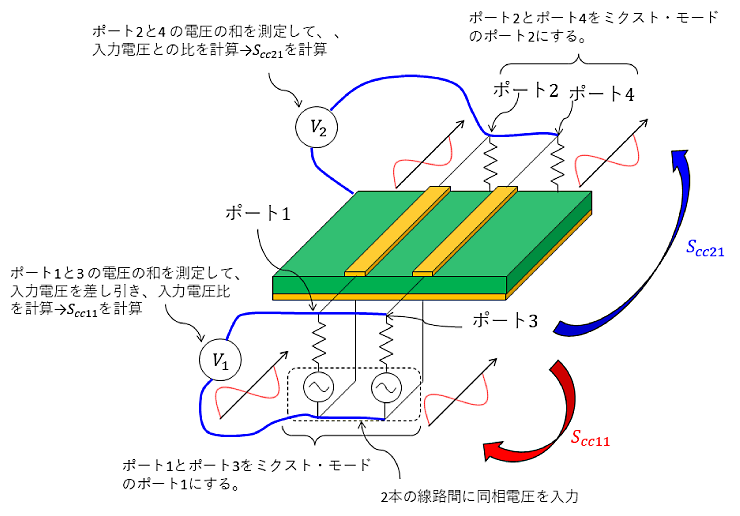
図6 $S_{cc11}$と$S_{cc21}$の測定方法。$S_{cc11}$:同相交流電圧入力に対する同相の反射係数。$S_{cc21}$:同相交流電圧入力に対する同相の透過係数。
$S_{dc11}$、$S_{dc21}$
図7 に示すように、$S_{dc11}$は同相電圧入力時の逆相電圧の反射比、$S_{dc21}$は同相電圧入力時の逆相の透過電圧比です。$S_{dc}$も配線構造が完全に対称であればゼロです。ゼロにならに理由は、$S_{cd}$と同じで配線長や配線幅が異なるのが原因です。
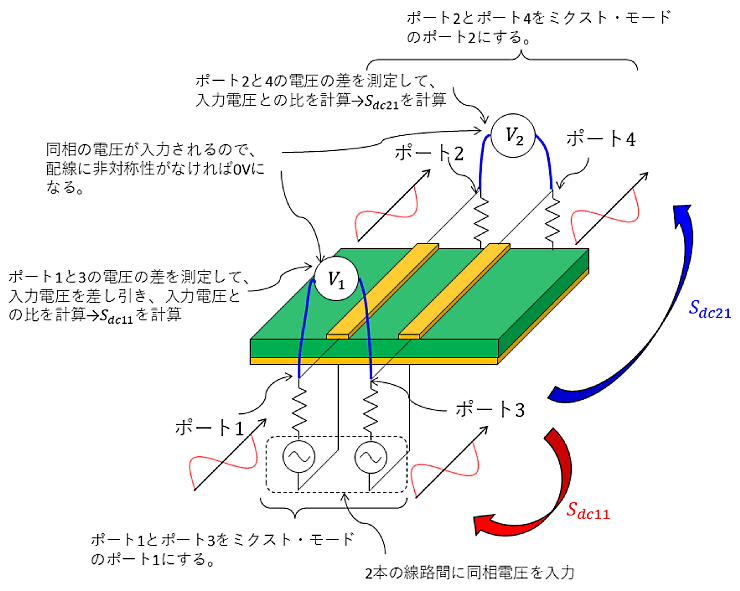
図7 $S_{dc11}$と$S_{dc21}$の測定方法。$S_{dc11}$:同相交流電圧入力に対する同相の反射係数。$S_{dc21}$:同相交流電圧入力に対する同相の透過係数。
参考文献
[1] Todd Hubing著、桜井 秋久ほか訳:デシベルから始めるプリント基板 EMC 即答 200、ZEP エンジニアリング株式会社。
[2] AI×電磁界シミュレータによる高速\&RF回路基板 スピード設計、ZEPエンジニアリング株式会社
[3] 川口 正、[VOD/KIT]ポケット・スペアナで手軽に!基板と回路のEMCノイズ対策 10の定石、ZEPエンジニアリング株式会社
[4] [VOD]高速&エラーレス!5G×EV時代のプリント基板&回路設計 100の要点、ZEPエンジニアリング株式会社
[5] [VOD] Gbps超 高速伝送基板の設計ノウハウ&評価技術、ZEPエンジニアリング株式会社
[6] [VOD]Before After!ハイパフォーマンス基板&回路設計 100の基本 【IoT・無線・通信編】、ZEPエンジニアリング株式会社